Práctica 10: Movimiento Rectilíneo Uniformemente Acelerado (MRUA)

OBJETIVO: Estudiar experimentalmente la posición y velocidad de un móvil con aceleración constante en función del tiempo.

INTRODUCCIÓN TEÓRICA:

Un cuerpo abandonado sobre un plano, inclinado un ángulo   respecto a la horizontal, se mueve con movimiento rectilíneo uniformemente acelerado (MRUA en adelante). Ello es debido a la componente paralela al plano de la aceleración de la gravedad.

Como s = ½·a·t2, la aceleración, a = 2s/t2, puede hallarse en función de los desplazamientos y de los tiempos tardados, y su valor debe ser, dentro de un margen de error, aproximadamente constante.
      

Por otra parte, las velocidades finales pueden hallarse a partir de

v = a·t

sin más que sustituir la a de la ecuación anterior

v = (2s/t2)·t = 2s / t

Las velocidades finales han de ser, por lo tanto, proporcionales a los tiempos, y los caminos recorridos proporcionales a los cuadrados de los tiempos.

Una alternativa es el análisis de video, que permite obtener de un video las trayectorias, y luego de éstas la velocidad y aceleración.

MATERIALES:

• Rieles de aluminio
• Tacos de madera
• Canicas
• Metro
• Cronómetro
• Rotulador

PROCEDIMIENTO:

1. Coloca el riel de aluminio apoyado sobre los tacos de madera con cierta inclinación.
2. Haz una marca en un extremo del riel y mide la distancia hasta el final.
3. Mide la inclinación haciendo el cociente entre la altura vertical de la que cae la bola y la distancia horizontal que recorre.
4. Deja caer una canica desde la marca, grabando con el móvil o el portátil el movimiento. Repítelo dos veces más.
5. Cambia la inclinación añadiendo tacos de madera hasta tener un total de cinco inclinaciones y tres repeticiones para cada una de ellas.

TAREAS:

1. Analiza los videos con Tracker o LoggerPro para obtener la aceleración en cada movimiento.
2. Promedia las aceleraciones de cada repetición para obtener un aceleración por inclinación.
3. Haz una tabla con tus datos.
4. Obten del programa un gráfico ejemplo de la posición frente al tiempo, de la velocidad frente al tiempo y de la aceleración frente al tiempo.
5. Haz un gráfico de la aceleración frente a la inclinación.
6. Comenta las gráficas obtenidas, comparando lo obtenido con lo previsto de acuerdo a la teoría. Evalúa la precisión de los datos a partir del ajuste de las gráficas a las líneas de tendencia.
7. Evalúa el procedimiento en cuanto a precisión y exactitud de los resultados. Expón detalladamente debilidades y fuentes de error del método y soluciones para las mismas.

RESULTADOS OBTENIDOS:

Posición (cm) frente al tiempo (s)

En la primera gráfica, cogida de la cuarta vez que realizamos el experimento, representa la posición en la que se encuentra la canica frente al tiempo transcurrido. Vemos que cuanto más tiempo pasa, mayor es la posición es de la canica, es decir, más ha avanzado. En la segunda fotografía podemos ver dos gráficas que representan lo mismo que la primera. En ellas se muestra una gráfica de la posición frente al tiempo con una aceleración positiva, y en la otra, con una aceleración negativa. Si comparamos la gráfica con aceleración positiva con la que hemos obtenido en nuestro experimento, podemos comprobar que nos ha salido la reacción esperada, es decir, que cuanto mayor tiempo pasa, mayor será la posición de la canica.

Velocidad (cm/s) frente al tiempo (s)

La gráfica superior corresponde a la relación entre la velocidad y el tiempo que existe en la segunda vez que llevamos el experimento a cabo. En ella vemos cómo aumenta la velocidad conforme avanza el tiempo, ya que, aunque hay muchos momentos en los que la velocidad de la canica disminuye, acaba aumentando de nuevo, haciendo que la velocidad final sea mayor a la inicial. Si comparamos esta fotografía con la segunda que nos encontramos abajo, podemos ver que el aumento de la velocidad es proporcional al paso del tiempo, que es lo que nos sale a nosotros en el experimento.

Aceleración (cm/s2) frente al tiempo (s)

En ambas gráficas podemos ver la relación entre la aceleración y del tiempo en el movimiento rectilíneo uniformemente acelerado. La primera es la gráfica obtenida en nuestra práctica. En ella podemos ver cómo la aceleración aumenta y disminuye frente al tiempo, sin embargo, también podemos observar que entre el crecimiento y decrecimiento de la misma, la aceleración se mantiene de manera relativamente constante. Si nos fijamos en la gráfica inferior, vemos cómo en el movimiento rectilíneo uniformemente acelerado la aceleración es siempre constante frente al tiempo, como lo es el resultado de nuestro experimento, más o menos.

Si observamos todas las gráficas que hemos obtenido en nuestro experimento, podemos ver que en todas ellas hay una línea de color rosa, que cruza con los resultados obtenidos. Esta es la línea de tendencia. Con ella podemos juzgar el camino que debería haber seguido nuestra gráfica. En la primera vemos que hay una línea recta que se desarrolla de forma creciente, al igual que la posición que nosotros hemos obtenido. Aunque el resultado no sea exactamente esta línea, comprobamos que es bastante acertado.

En la segunda gráfica, también vemos que la línea rosa es ascendente, de modo que cuanto mayor tiempo transcurre, mayor es la velocidad. Aunque la velocidad que nosotros hemos obtenido tiene puntos tanto por encima como por debajo de esta línea de tendencia, comprobamos que el resultado es el mismo: al final, tanto la línea de tendencia como los resultados que nosotros hemos obtenido, tienen una velocidad final mayor a la que se tiene al comienzo del experimento.

Finalmente, en la última gráfica, en la que se relaciona la aceleración frente al tiempo, vemos que la línea de tendencia aumenta ligeramente conforme pasa el tiempo, pero podemos considerar que es prácticamente constante. Aunque no es fácil apreciarlo, los resultados que nosotros hemos obtenido en nuestro experimento no se diferencian mucho de la línea de tendencia. Esto es porque, a pesar de crecer y decrecer con frecuencia, se mantiene de manera más o menos constante, ya que siempre acaba pasado por los mismos valores.

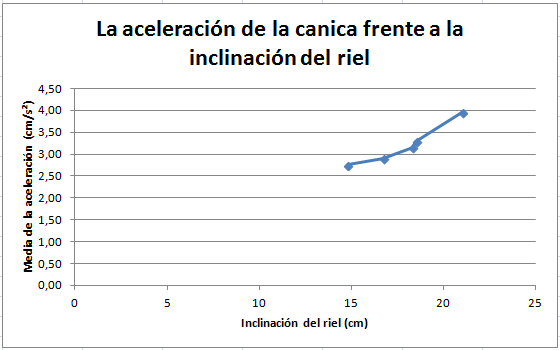
Aquí podemos ver una tabla y una gráfica en las cuales vemos a la aceleración de la canica frente a la inclinación del riel por el que rodaba:

Relación entre la aceleración de la canica y la inclinación del rie

Tanto en la tabla como en el gráfico podemos observar que cuanto mayor sea la inclinación del riel, mayor será la aceleración de la canica, y viceversa.

CONCLUSIÓN:

En conclusión, podemos decir que, en el movimiento rectilíneo uniformemente acelerado, tanto la posición como la velocidad de la canica aumentan a medida que pasa el tiempo, mientras que la aceleración se mantiene relativamente constante durante el experimento.

EVALUACIÓN: